5 The Membrane at Rest
As covered in the previous chapter, at rest there is an uneven distribution of ions on either side of the membrane. The inside of the membrane is more negatively charged than the outside, which is expressed as a negative membrane potential.
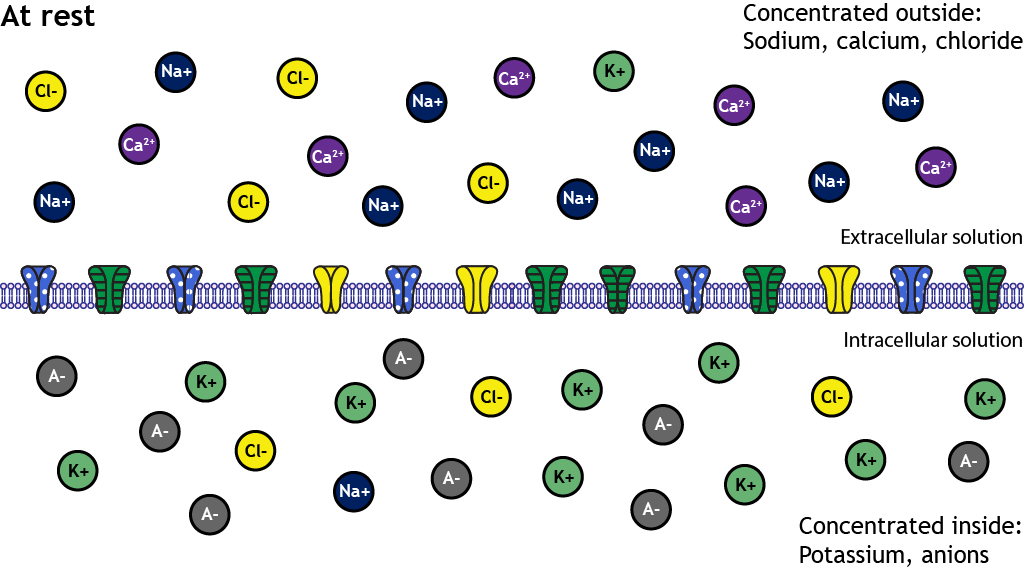
The membrane at rest is most permeable to potassium. Permeability for other ions, like chloride and sodium, is significantly lower.
Permeability at Rest
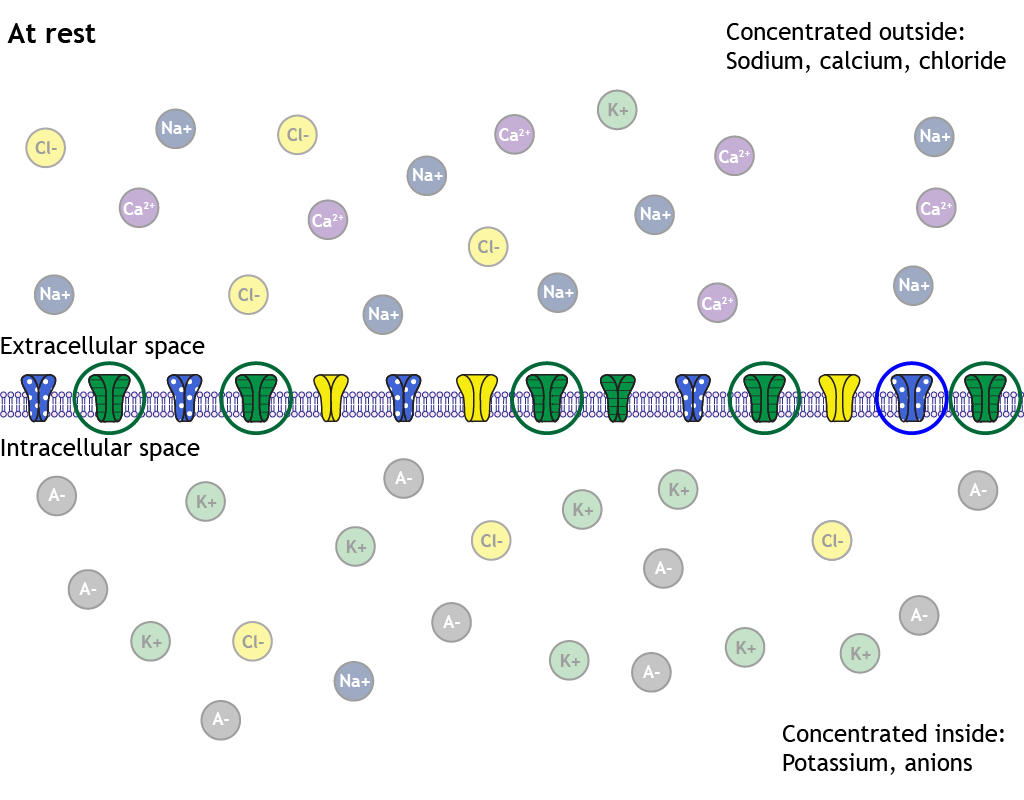
How the ions are distributed across the membrane plays an important role in the generation of the resting membrane potential. At rest a type of non-gated ion channels, called leak channels are actually open. Significantly more potassium channels are open than sodium channels, and this makes the membrane at rest far more permeable to potassium than sodium.
Potassium Can Cross Membrane at Rest
Since the membrane is permeable to potassium at rest due to the open non-gated channels, potassium ions flow across the membrane. Since permeability to potassium is hundreds of times more than that to sodium, the electrochemical gradients at work will cause potassium to flow out of the cell in order to move the cell's membrane potential toward potassium's equilibrium potential of -80 mV.
Resting Membrane Potential Value
You might ask, though, if the cell has these open non-gated ion channels, and ions are moving at rest, won't the cell eventually reach potassium's equilibrium potential if the membrane is only permeable to potassium?
If the only structural element involved in ion flow present in the cell membrane were the open non-gated potassium channels, the membrane potential would eventually reach potassium's equilibrium potential. However, the membrane has other open non-gated ion channels as well. There are fewer of these channels compared to the potassium channels, though. The permeability of chloride is about half of that of potassium, and the permeability of sodium is about 25 to 40 times less than that of potassium. This leads to enough chloride and sodium ion movement to keep the neuron at a resting membrane potential that is slightly more positive than potassium’s equilibrium potential.
The sodium-potassium pumps work to keep the ion concentrations stable even as ions cross the membrane at rest.
Maintenance of Gradients
As ions move across the membrane both at rest and when the neuron is active, the concentrations of ions inside and outside of the cell will change. This leads to changes in the electrochemical gradients that are driving ion movement. What, then, maintains the concentration and electrical gradients critical for the ion flow that allows the neuron to function properly?
The key mechanism for maintaining gradients across the neuronal membrane is the sodium-potassium pump. The pump uses energy in the form of ATP to move three sodium ions out of the cell and two potassium ions in. This moves the ions against their electrochemical gradients, which is why it requires energy. The pump functions to keep the ionic concentrations at proper levels inside and outside the cell. The sodium-potassium pump is so critical to function, that it uses fully 30-40% of the brain's energy consumption.
Calculating Membrane Potential with Goldman Equation
It is possible to calculate the membrane potential of a cell if the concentrations and relative permeabilities of the ions are known. Recall from the last chapter, the Nernst equation is used to calculate one ion’s equilibrium potential. Knowing the equilibrium potential can help you predict which way one ion will move, and it also calculates the membrane potential value that the cell would reach if the membrane were only permeable to one ion. However, at rest, the membrane is permeable to potassium, chloride, and sodium. To calculate the membrane potential, the Goldman equation is needed.
The Goldman Equation
[latex]V_{m}=61 * \log \displaystyle \frac{P_{K}\left[K^{+}\right]_{\text {outside }}+P_{N a}\left[N a^{+}\right]_{\text {outside }}+P_{C l}\left[C l^{-}\right]_{\text {inside }}}{P_{K}\left[K^{+}\right]_{\text {inside }}+P_{N a}\left[N a^{+}\right]_{\text {inside }}+P_{C l}\left[C l^{-}\right]_{\text {outside }}}[/latex]
Like the Nernst equation, the constant 61 is calculated using values such as the universal gas constant and temperature of mammalian cells
Pion is the relative permeability of each ion
[Ion]inside is the intracellular concentration of each ion
[Ion]outside is the extracellular concentration of each ion
Example: The Neuron at Rest
[latex]V_{m}=61 * \log \displaystyle \frac{P_{K}\left[K^{+}\right]_{\text {outside }}+P_{N a}\left[N a^{+}\right]_{\text {outside }}+P_{C l}\left[C l^{-}\right]_{\text {inside }}}{P_{K}\left[K^{+}\right]_{\text {inside }}+P_{N a}\left[N a^{+}\right]_{\text {inside }}+P_{C l}\left[C l^{-}\right]_{\text {outside }}}[/latex]
| Ion | Inside concentration (mM) | Outside concentration (mM) | Relative permeability |
|---|---|---|---|
| Sodium | 15 | 145 | 0.04 |
| Potassium | 125 | 5 | 1 |
| Chloride | 13 | 150 | 0.4 |
[latex]V_{m}=61 * \log \displaystyle \frac{1[5]+0.04[145]+0.4[13]}{1[125]+0.04[15]+0.4[150]}= -65 mV[/latex]
Key Takeaways
- At rest, the membrane is most permeable to potassium because Non-gated (leak) potassium channels are open at resting potential
- Other ion channels (chloride and sodium) are also open, but fewer are open than potassium
- Therefore, the resting membrane potential of a typical neuron is relatively close to the equilibrium potential for potassium (EK)
- Electrochemical gradients needed for normal neuronal function are maintained, despite constant flow through leak channels, by the sodium-potassium pump, which expends energy to translocate K+ into the cell, and Na+ out of the cell.
Test Yourself!
- From memory, draw a diagram of a neuronal membrane at rest that includes the non-gated ion channels in their correct state (i.e., open, closed, inactivated).
- If all other conditions (see purple box above) are unchanged, but PNa is 0.004 instead, how will the resting potential change?
Video Lecture
Attributions
This chapter was adapted from "The Membrane at Rest" in Foundations of Neuroscience by Casey Henley which is licensed under a Creative Commons Attribution NonCommerical ShareAlike 4.0 International License.