Transcript

Overview

The comic is drawn in a smooth geometric cartoony style and colored in a limited, blue-heavy palette. Most of the backgrounds are a deep navy.

Cover

The Bell Game: Beating the Odds with Quantum Entanglement

Michael Raymer and Margaret Kyser

The University of Oregon Science and Comics Fellowship Program

Celebrating the 2022 Nobel Prize in Physics [a small Nobel Prize medal is next to this line]

Cover Description: The cover has an abstract purple gradient; two diagrams of atoms are connected by a glowing filament. Two scientists stand near the atoms. One is a short woman with dark skin and a brunette bob wearing a long sleeve polo and slacks, the other is a taller woman with tan skin and grey hair in a low bun, glasses and an unbuttoned collared t-shirt over a black top.

Page 1

Panel 1: “Welcome to Bell’s Casino! Today we’re playing the Bell Game.” Most of the panel shows a blueprint. A “you are here” marker shows that “you” are in a hallway. A large room with a stage and a screen adjoins the hallway. On the stage are doors to two rooms (room 1 and room 2), and inside each room is a rectangle. In the foreground of the panel are the head and shoulders of two young men walking through the hallway.

Panel 2: We are now in the room depicted in the blueprint in the previous panel. Two people stand on stage. One is a woman with a long black ponytail, wearing a knee length skirt and a sweater vest over a collared shirt and tie. The other is a man with a thick mustache and beard, wearing a matching outfit with slacks instead of a skirt. They are both holding clipboards, wearing headset mic and yellow buttons that say “host.” Behind them are the two doors and the screen. In front of the stage are the silhouettes of a crowd.
The woman continues speaking, “Earn money and impress your friends!”

Panel 3: A close-up of the woman on stage, holding her clipboard, “Here are the rules…”

Panel 4: “People from the audience will come up in pairs. Behind me are two isolation rooms…Each player will go to Room 1 or Room 2, which each have a gambling machine. The machines each have two levers, one Red and one Green, that you can pull up or down.”

The woman gestures towards an inset panel showing one of the machines. It looks like a slot machine with a red lever on the left side and a green lever on the right, a screen on the console between the levers with four places to show results, and an embellished title at the top of the machine, “The Bell Game.”

Page 2

Panel 1: The other host starts talking, “Each player will pay a $1 entry fee ($2 between the two players) and get four tries. We’ll each flip a coin indicating which lever, Red or Green, the players will pull. Each player chooses whether to pull up or down, though.” A coin flips through the air. It’s red on one side and green on the other.

Panel 2: A close up on the bearded host’s face. “Also — no communication is possible between the two players or between us, the hosts. However, players are free to strategize together before going into their separate game rooms. They can also carry a notebook or other device with them, as long as their tools don’t allow any outside communication.

Panel 3: He continues, “Players must pull up or down roughly half the time, but the sequence can be anything – including a coordinated sequence planned before the game begins. The scoring rules for winning or losing points are shown on the screen behind us.” Both hosts stand on stage near the doors, tiny beneath the enormous screen. The screen is partially obscured by text balloons but the visible text reads, “3. If both hosts indicate to pull the Green…both pull Up or both pull Down, they…”

Page 3

Panel 1: A close-up on the screen showing the scoring rules.

“Scoring Rules”

“If both hosts indicate to pull the Red levers, and the players both pull Up or both pull Down, they win one point ($1), If they pull different, they lose a point (-$1).” [symbols indicate two red levers, both pulled up or down.]

“If the hosts indicate to pull opposite-color levers, and the players both pull Up or both pull Down, they win one point ($1), if they pull different they lose a point (-$1).” [symbols show one red lever and one green lever, both pulled up or both down]

“If both hosts indicate to pull the Green levers, and the players both pull Up or both pull Down, they lose one point (-$1). If they pull different, they win a point ($1). [Symbols indicate two green levers, both pulled up or down.]

Panel 2: The bearded host appears in an inset round panel, gesturing upward, “after each set of four tries, the players’ sequences of ups and downs will be sent to our central computer, which tallies up the net score and announces the winnings or losses for that set. This process happens 99 more times, for a total of 100 four-try sets.”

Page 4

Panel 1: In the foreground the host with the ponytail addresses the audience, “Our first pair of contestants is Claire and Dinesh!” A round insert showing Claire and Dinesh. Claire has short red hair, pale freckled skin, and is wearing a white button down and a yellow tie. Dinesh is taller than Claire, has dark hair and brown skin and is wearing a maroon long sleeve polo.

Panel 2: Claire and Dinesh walk towards the stage. Claire: “Common sense tells me that the best strategy is probably to always pull the same way.” Dinesh: “Yeah, I agree. I think we’d win about three out of four tries that way, but we’d need to coordinate our pulls somehow. Remember that we need to pull up around half the time, and down around half the time…”

Panel 3: Claire and Dinesh continue their conversation, Claire: “Well, why don’t we just alternate pulling up and down forever?” Dinesh: “Sure, that sounds good! Let’s start by pulling up, no matter what color lever we have to pull.”

Panel 4: Claire enters room 1 with the ponytail host, Dinesh walks towards room 2 with the bearded host.

Page 5

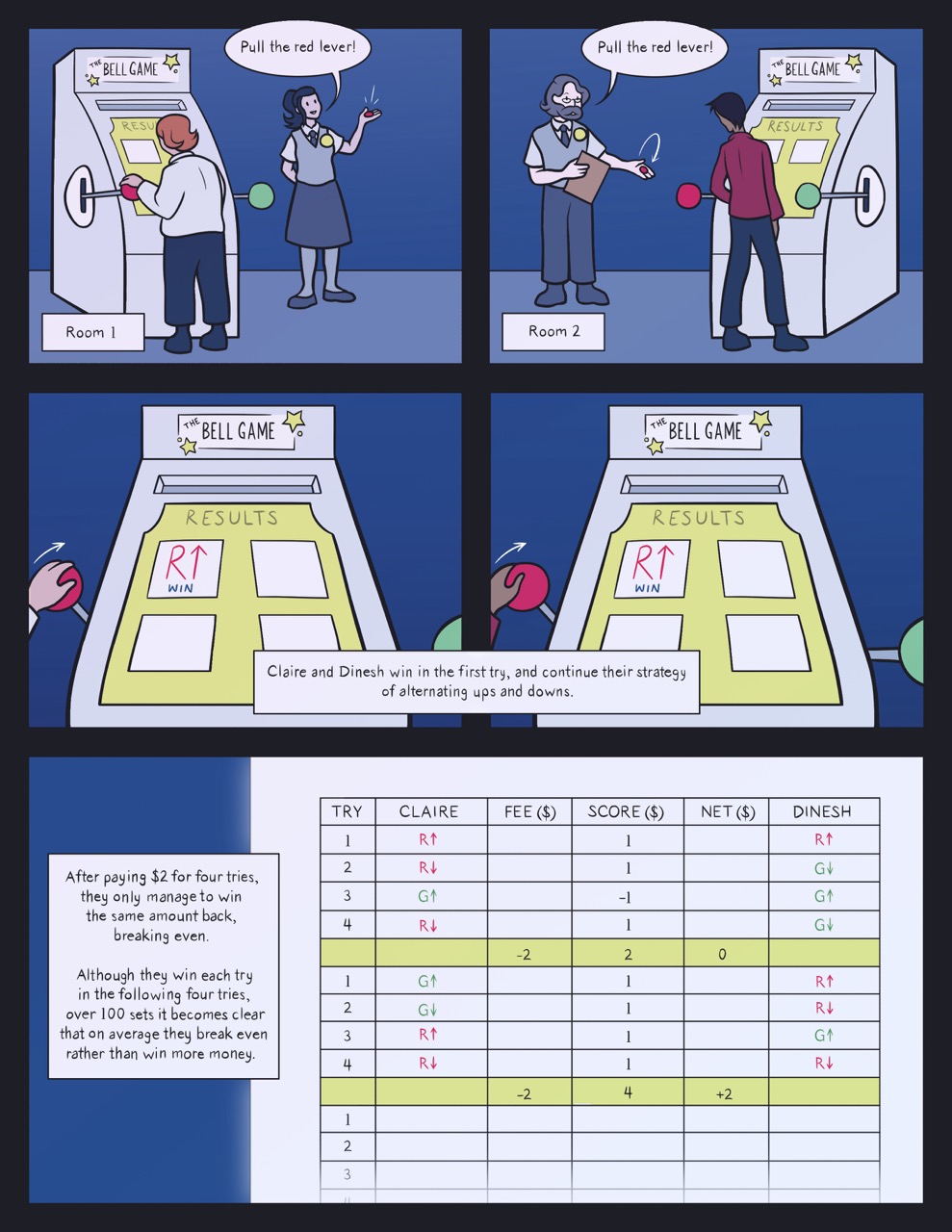
Panel 1: “Room 1” Claire stands at a Bell Game machine (described on page 1). The host flips her red/green coin and tells Claire to “pull the red lever!”

Panel 2: “Room 2” Dinesh stands in front of an identical machine. The host flips his coin and tells Dinesh to “pull the red lever!”

Panel 3: Claire pulls the red lever up, on the results pane of the Bell Game machine, the first of four results screens shows the result “R [up arrow] Win”

Panel 4: Dinesh also pulls the red lever up; his machine shows an identical win result in box 1. “Claire and Dinesh win in the first try, and continue their strategy of alternating ups and downs.”

Panel 5: “After paying $2 for four tries, they only manage to win the same amount back, breaking even. Although they win each try, in the following four tries, over 100 sets it becomes clear that on average they break even rather than win more money.”

A table shows 2 rounds (or four tries), in the first round Claire and Dinesh break even, in the second round they are up 2 points / $2. The table continues (presumably over 100 sets) but is not visible past the second round.
Full Table (lightly adapted for clarity):

Page 6

Panel 1: Narration: “At last, the two leave their isolation rooms and return to the crowd.” Dinesh and Claire walk down off the stage, looking disappointed. Dinesh: “There has to be a better strategy to win more.” Claire: “hmm…”

Panel 2: A close-up on Claire, holding a notebook, “actually, the more I think about it, I’m pretty sure there is no better pre-planned strategy. Let’s write out other possibilities…”

Panel 3: Claire studies her notebook, “By only pulling the same like we did, players will typically break even. It’d turn out the same way on average even after hundreds or thousands of tries.”

Panel 4: Claire and Dinesh both look at Claire’s notebook. Dinesh: “I see…after paying the fee of $2 for four tries, players can only win an average of $2 back, so the game is pointless.” Claire: “Yeah, and always pulling in the opposite direction would be even worse. We would have lost money that way.” Claire’s notebook shows a table with the results for the same two rounds, but in the case where Claire and Dinesh pull in opposite directions. This time they lose $4 in the first round and $6 in the second round.

Page 7

Panel 1: Narration: “the hosts also return from the isolation rooms.” The hosts stand on stage outside their respective rooms. Ponytail host: “Well, that was fun! Are there any more takers? I think I see two approaching the stage.” Bearded host: “Yes…but what are those devices they’re holding?”

Panel 2: The two scientists from the cover walk on stage. Alicia is a woman wearing slacks and a long sleeve polo with a shoulder length bob and dark skin. Bette is a woman wearing an unbuttoned short sleeve t-shirt and slacks with a low grey-bun, tan skin, and glasses. Both women hold nondescript light blue boxes, similar in size to the hosts’ clipboards. Alicia: “These are Quantum Memory Modules!” Ponytail host: “Say what?” The hosts look confused.

Panel 3: Alicia and Bette talk to the hosts. Bette: “We prepared them as part of our strategy before arriving. But don’t worry, they won’t communicate to anything outside the room they’re in. No internet connection, for example. Ponytail host: “Oh, we’re not worried about that. The casino built the isolation rooms at great expense. The walls are light tight, sound proof, radio proof, and sealed against every form of signaling known to physicists – even gamma rays, cosmic rays, and neutrinos. Just in case. And we have no concerns about gravitational waves – they’re way too weak.” Bette: “No problem!”

Page 8

Panel 1: “Earlier…” Alicia: “First, let’s load these quantum entangled pairs of atoms into the memory device.” Narration: “Alicia and Bette in their physics lab planning their strategy.” Alicia and Bette are both wearing lab coats, standing in a lab. On the lab bench is a machine that has a long arm with a cup on it, and a rectangular box with a divider.

Panel 2: Alicia: “Even after we pull this device apart, the pairs of particles will remain entangled. All we have left to do is attach the front panels and separate it into two devices.” Alicia looks at the open-top rectangular box; there are two symbols representing entangled atoms connected with a line to two other atoms on the other side of the box.

Panel 3: The single rectangular box with a divider is split into two separate boxes, and lids are attached so they are no longer open at the top.

Panel 4: Narration: “When Alicia and Bette press the button corresponding to the lever they must pull, their devices give them instruction.” The two devices are finished. Each device has a red button and a green button and a small screen. Four white circles on each device are connected to corresponding circles on the other device with a white line, representing entangled atoms.

Page 9

Panel 1: Alicia is in Room 1 with the ponytail host standing in front of the Bell Game machine holding her device. The host flips her coin, “pull the red lever!”

Panel 2: In Room 2 Bette stands in front of an identical machine holding her device. The other host flips his coin, “pull the red lever!”

Panel 3: Alicia’s device says “pull down.” The Bell Game machine shows “Red down, win” in the first result box.

Panel 4: Bette’s device says “pull down.” The Bell Game machine shows “red down, win” in the first result box.

Panel 5: Narration: “Using their Quantum Memory Modules, Alicia and Bette win whenever possible. They win back and average $2.83 for every $2 paid, or net winnings of $0.83 for each set of four tries. After 100 sets of four tries, they win $83!” The ponytail host faces away from the reader, holding her clipboard. She is surprised. Her clipboard reads: 0.83 x 100 = $83.

Page 10

Panel 1: “Back on the stage…” The ponytail host looks concerned, “Winning back an average $2.83 per $2 paid is suspiciously lucky. The first players could only break even – I bet that you two were cheating!” Bearded host: “Yeah! No one ever beats the Bell Game so consistently. What’s going on with those strange devices?”

Panel 2: Alicia: “Actually, in our devices, quantum entanglement creates correlations that are stronger and better than you could achieve by using your common sense or ‘classical physics’ – that is, non-quantum physics.” Alicia gestures toward a diagram of two atoms connected by a white line.

Panel 3: Bette: “Yes, the devices don’t even communicate! The Quantum Memory Modules can store quantum information that is inherently entangled. No communication is needed between the modules once they’ve been ‘quantum-programmed.’” Bette holds her module next to a diagram showing four atoms connected to four more corresponding atoms.

Page 11

Panel 1: The ponytail host: “Interesting. Is there any way for our casino to shield against that kind of quantum entanglement?” Alicia, shrugging: “No. As far as any physicist knows, that’s impossible. The host and Alicia stand on either side of a diagram showing four unbreakably entangled atoms.

Panel 2: Bearded host: “Where can I get a set of those devices?”

Panel 3: Bette: “You’d have to build your own! No company sells them yet. These two were made in a university lab funded by the National Science Foundation after the government invested over $1 billion in research over the past 20 years. In fact, Alicia and I are both physics PhD candidates at the university, where cool quantum research is always taking place. You two could join us!

Panel 4: The bearded host looks skeptical, “I’m not sure about that. Everyone knows physics is hard…” Bette and Alicia smile. Bette: “Well, so is learning to be a great basketball player. It’s fun, and people do it all the time!”

Page 12

[a full page of text]

Dear Reader,

You’re probably wondering what was in the hand-held devices Alicia and Bette carried into the rooms that allowed them to win the Bell Game. Is the story science fiction? No! The story could happen exactly as presented, with the exception that we don’t yet have portable quantum memory devices available. Quantum memory devices do exist now in quantum physics labs around the world, but they are large, bulky, and not portable. Scientists think it’s only a matter of time before miniaturized versions become available.

But, you might ask, what is an entangled state and how does it allow Alicia and Bette to win the game? And do the devices have to be operating by quantum physics principles? Why not two preprogrammed conventional calculators, each having the proper set of instructions that Alicia and Bette are to follow in deciding to pull a lever up or down?

Physicists know that, according to the theory of quantum mechanics, no such devices can be made without controlling matter at the quantum (that is, atomic) level. A conventional calculator (or your phone) stores only conventional (classical) bits of information: 0 or 1. Entanglement of such bits is impossible. Yet at the quantum level, where bits can be stored in single atoms, entanglement is possible. We call such quantum bits qubits. A single qubit can store both possibilities 0 and 1 simultaneously. More importantly, two qubits can be prepared in an entangled state (as Alicia and Bette did in their lab before playing the game) such that, for example, if their values (0 or 1) are read, they will both be 0 or both be 1, even though the outcomes are random with 50/50 probabilities.

That situation is not the same as Claire and Dinesh deciding their strategy with prearranged lists of instructions to always pull up or down together. In the case of entangled qubit instructions, the decisions to pull up or down are not prearranged; the instructions are created spontaneously when needed and are seemingly random. When the players are told by the hosts which lever to pull, each player enters that information into their device and the devices pop up with instructions for which way to pull. In every case the players sometimes win and sometimes lose. Now, though, their overall chance of winning each try is around 85%, instead of 50% as it was in the conventional scenario. For every four tries costing $2, they win around $2.83 on average.

The quantum devices allow Alicia and Bette to beat the conventional odds by using entanglement. It seems like a magic trick because it appears as though the devices “know” what is going on in the other room, even with no possible communication between them. However, it really can work as described in the story using quantum physics and quantum engineering. This type of entanglement has been confirmed by physics experiments carried out in many laboratories.

Page 13

[Two entangled atoms (A and B) are connected by a string. Alicia’s and Bette’s hands gesture towards the atoms.]

How does quantum entanglement enable new forms of technology not possible using classical (non-quantum) principles? A key word here is information. When we talk about ‘what you know’, we mean what information you possess. Classical information is what can be expressed, for example, by symbols written on paper such as the words in this comic. Quantum information, on the other hand, cannot be expressed that way. It can be expressed only by preparing atomic-scale entities such as atoms or photons (that is, light) in special entangled states.

Physicists know how to ‘teleport’ entangled states of one set of objects to another set of objects. This doesn’t mean they transport the objects themselves – only the information about the object is teleported. This kind of information transfer is what quantum computers will need to communicate among themselves and is what gives quantum computers a big advantage over ordinary computers for solving certain kinds of mathematics problems.

The 2022 Nobel Prize honored the physicists who verified that quantum entanglement is actually an aspect of the world we live in and opened the door for many new applications to come.

Page 14

If you’d like to dive deeper into the ideas of quantum entanglement and how it works in the Bell Game, in cryptography, and in computing, you can earn all about it in a book by one of this comic’s authors, Michael Raymer: Quantum Physics: What Everyone Needs to Know. Find the book by scanning the QR code [QR excluded in transcription, link embedded in book title].

Another accessible book which describes the Bell Game is Nicolas Gisin’s Quantum Chance: Nonlocality, Teleportation and Other Quantum Marvels.

This work was supported by the National Science Foundation through the University of Oregon Science and Comics Fellowship Program (grant 1944826-PHY) and the University of Arizona Engineering Research Center for Quantum Networks (grant 1941583)

Page 15

Text continues: “The 2022 Nobel Prize in Physics was awarded to Alain Aspect, John Clauser, and Anton Zeilinger for experiments showing that quantum entanglement across macroscopic distances can create measurement correlations that defy any ‘classical-physics’ description. Mysteriously, such correlations exist without any physical, non-local interaction mechanism, yet they are the basis of the newly emerging possibilities offered by quantum technologies.”

Line drawing of John Clauser, an older man with short hair, “It was the quest to understand quantum mechanics that has kept me going all this time.”

Line drawing of Anton Zeilinger, a middle-aged man with slightly long short hair and glasses, “Quantum teleportation is a child of science fiction in a sense. The mistake they made is they thought in order to teleport somebody you have to teleport the substance you are made of. We found it’s enough to transport the quantum state – the embodiment of all information which characterizes you. It’s a means of transporting the output of one quantum computer to the input of another quantum computer.”

Line drawing of Alain Aspect, a man with a large mustache, short hair and square glasses. “I’m sure I am not good at going to applications myself. But I explained what I have been doing as basic science, and people around listen to it and say – Oh, we could use that for something.”
Quotes from Nobel Minds 2022 [YouTube Video]